Ceptr Blog

Everything in Ceptr gets built out of semantic trees. Why? Alan Perlis' epigram #106 on programming hints at the answer:

It's difficult to extract sense from strings, but they're the only communication coin we can count on.

Ceptr creates a new "communication coin" that we can still count on (in both senses) but from which it's much much easier to "extract sense." In fact, the "sense" gets baked in at the bottom layer in that everything in Ceptr is built out of semantic trees. Extracting "sense" however has lots to do with pattern matching. Regular Expressions provide a rich expressive capacity for discovering the patterns in text. We have build Semantic Tree Regular Expressions (Semtrex), as way to do the same for our semantic trees.

As a first introduction to Semtrex, you should read Marc Clifton's very good and detailed article. It gives some good backstory on semantic trees with examples. In this post I want to share a little about some of the coding issues involved in implementing them, which I'm very familiar with at the moment because of some bugs that recently showed up in my code!

My implementation is heavily based on the code and theory provided by Russ Cox's great article on regular expression matching. As he describes, regular expression implementations usually convert the regular expression to a state machine that then gets run against a string to see if it matches. For example, from Cox's article here's the state machine for the regex abab|abbb:

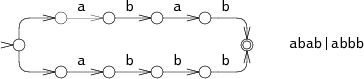
In these state diagrams a labeled transition means: read a character and if it matches the label, move to the next state. As he explains in the article, for any state that has two branches we can theoretically assume that the machine that magically chooses the correct branch for any given string. Practically we implement this magic by trying both branches either sequentially with a backtracking algorithm, or by running both branches simultaneously.

Now here's the thing about regular expressions for semantic trees: because trees are not linear (like strings) the transition from one state to the next also has to include some instructions about how move through the tree.

Here's an example state diagram for the Semtrex: /A/(B|C/D,E)

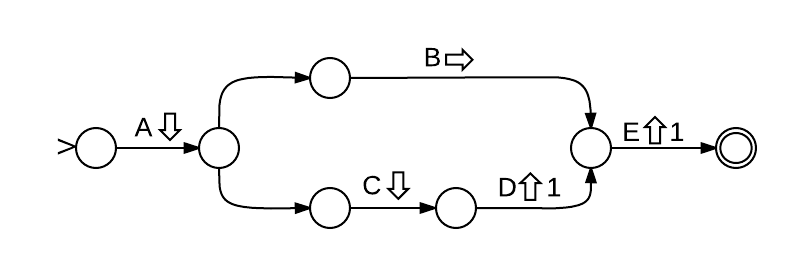
(Note that any up arrows which pop up the number of levels indicated do also have an implied next child as well.)

Debugging the code that runs this machine is tricky, because it's hard to see the state of the whole machine in gdb debugger. What I did to make this easier was come up with a textual representation for the state machine. The machine above looks like this:

(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]

Each state is an item in parens. If the state has a transition that matches a symbol the symbol is in the parents. Special states are splits (s) and match (m). The trick about splits is how to represent both branches. What you see is that one of the branches follows right out of the split, but the second comes later in square brackets. The outgoing arrow just points to "X", which means some other part of the tree, so you have to know which… I know kinda ugly, but it's enough for debugging

Below is actual debugging output (only slightly doctored) of that machine being run against the tree (A (C (D)) (E)). The output uses ANSI color coding to show in red the current state and tree position.

D_STX_MATCH: IN:Symbol
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: transition: down
D_STX_MATCH: IN:Split
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: pushing split branch for backtracking to state (C)
D_STX_MATCH: IN:Symbol
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: Fail: so popping to--(C (D))
D_STX_MATCH: IN:Symbol
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: transition: down
D_STX_MATCH: IN:Symbol
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: transition: popping -1
D_STX_MATCH: IN:Symbol
D_STX_MATCH: FSA:(A)-Down->(s)-->(B)-Next->(E)-Up1->(m)[-->(C)-Down->(D)-Up1->X]
D_STX_MATCH: tree:(A (C (D)) (E))
D_STX_MATCH: transition: popping -1
D_STX_MATCH: Matched!

Adding this visualization was enough for me to find the bug I was having where the state machine wasn't popping back up enough in some circumstances, and it's revealed another bug that I'm still working on in the case of grouping where we collect up matched data.

If this kind of stuff intrigues you, feel free to show up and ask questions at one of our bi-monthly dev chats which happen every 1st and 3rd Wednesday of the month at 3pm Eastern/Noon Pacific.

Hope to see you there!